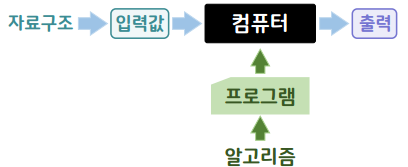
01. 배열의 정의
✅ 배열
- 메모리 공간(메인 메모리, DDR)에 저장되는 원소의 물리적인 위치를 순차적으로 결정
- 배열의 순서 == 메모리 공간에 저장되는 원소값의 물리적 순서
- 원소들은 모두 같은 자료형과 같은 크기의 기억 공간을 가짐
- 인덱스와 원소값(<index, value>)의 쌍으로 구성된 집합

- 인덱스(index)
- 컴퓨터의 내부구조나 메모리 주소와 무관하게 개발자에게 개념적으로 정의됨(추상화된 값) → 불변
- 보통 배열의 인덱스는 0부터 시작
- 인덱스를 이용해서 원소값에 접근하기 때문에 직접 접근 가능
- 메모리 주소값은 실제 메모리의 물리적인 위치값(주소값)
- 실제로 연속된 메모리에 저장됨
- 주소값은 가변적임(시간이 지나거나 프로그램을 실행할 때마다 변경됨)
02. 배열의 추상 자료형
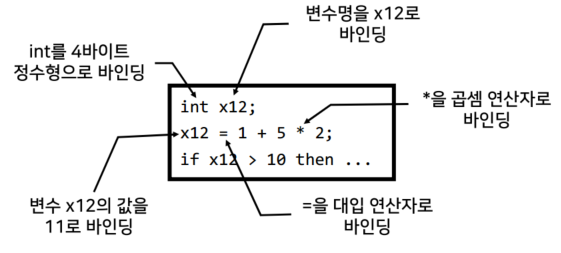
▪️ 추상자료형: 객체 및 관련된 연산의 정의
예를 들어 C언어의 printf() 처럼 C 컴파일러 개발자가 만들어 놓은 것을 다른 개발자들은 가져다 쓰기만 하면 되는...
▪️ 자료형: 메모리 저당 할당을 위한 선언
int, float, ...
'내가 프로그래밍에서 이 변수에 대해서 이러한 메모리 영역을 할당받고 싶어'라고 선언하는 것
🔸ADT Array 객체
- < i∈Index, e∈Element > 쌍들의 집합
- Index: 순서를 나타내는 원소의 유한집합
- Element: 타입이 같은 원소의 집합
🔸연산
| a∈Array; i∈Index; item∈Element; n∈Integer; |
- a: 0개 이상의 원소를 갖는 배열
- item: 배열에 저장되는 우너소
- n: 배열의 최대 크기를 정의하는 정수값
03. 배열의 연산의 구현
※ 컴파일러 개발자의 역
▪️ 배열 생성
//① Array create(n) ::= 배열의 크기가 n인 빈 배열을 생성하고 배열을 반환;
void create(int *a, int n){ //n=5
int i;
for(i=0, i<n, i++){
a[i] = 0;
}
}
▪️ 배열 생성 결과

▪️ 배열값 검색(retrieve 연산)
/*
② Element retrieve(a, i) ::= if(i∈Index) then{
배열의 i번째에 해당하는 원소값 'e'를 반환;
}else{
에러 메세지 반환;
}
*/
#define array_size5
int retrieve(int *a, int i){ //i=2
if(i>=0 && i<array_size){
return a[i];
}else{
printf(Error\n);
retrun(-1);
}
}
▪️ 배열값 검색 결과

▪️ 배열값 저장(store 연산)
/*
③ Array store(a, i, e) ::= if(i∈Index) then{
배열 a의 i번째 위치에 원소값 'e'를 저장하고 배열 a 반환;
}else{
인덱스 i가 배열 a의 크기를 벗어나면 에러메세지 반환;
}
*/
#define array_size 5
void store(int *a, int i, int e){ //i=3, e=35
if(i>=0 && i<array_size){
a[i] = e;
}else{
printf("Error\n")
}
}
▪️ a[3]의 값이 35로 변경되어 저장된 모습

04. 1차원 배열 및 배열의 확장
✅ 1차원 배열


- 한 줄짜리 배열을 의미하며 하나의 인덱스로 구분됨
- A[]의 시작주소값을 a라고 가정하면, A[i] 저장 주소는 [a+i*k]가 됨(k: 메모리할당단위)
- 운영체제가 이러한 규칙을 기반으로 데이터에 접근
✅ 행렬의 배열 표현


- 행렬을 컴퓨터에서 표현하기에는 2차원 배열(1차원 배열을 여러 개 쌓아 놓은 것)이 적합함
🔸행 우선 배열

🔸행 우선 할당
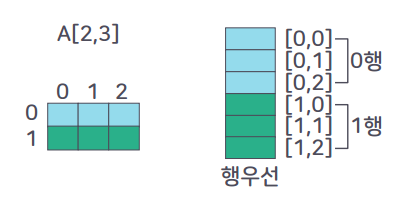
- 가로의 1차원 배열 단위로 메모리 영역을 우선 할당함
🔸열 우선 배열

🔸열 우선 할당
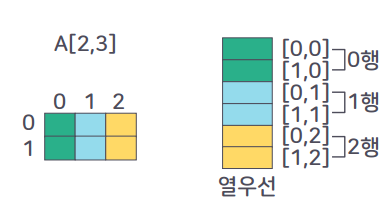
- 세로의 1차원 배열 담위로 메모리 영역을 우선 할당함
🔸C언어에서의 2차원 배열(행 우선 순서 저장)
- C언어에서 A[5][3]을 선언하면 다음과 같은 배열 생성
- 사용하는 언어가 어떠한 배열 저장 규칙을 갖고 있는지를 알면 좀 더 향상된 프로그램 실행 속도를 찾아낼 수 있다!
| 0, 0 | 0, 1 | 0, 2 | 0, 3 | 0, 4 |
| 1, 0 | 1, 1 | 1, 2 | 1, 3 | 1, 4 |
| 2, 0 | 2, 1 | 2, 2 | 2, 3 | 2, 4 |
05. 희소행렬의 개념
✅ 희소행렬

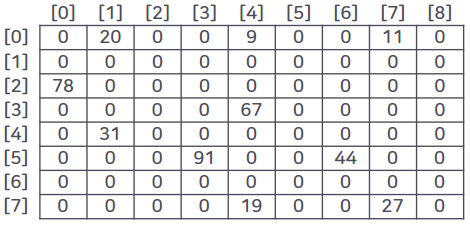
- 원소값이 0인 원소가 그렇지 않은 원소보다 상대적으로 많음
- 메모리 낭비를 막고 효율성을 높이기 위해서 0인 원소는 저장하지 않고 0이 아닌 값만을 따로 모아서 저장하는 방법이 필요 => 희소행렬(추상화를 한 번 더한 것)

'KNOU > 자료구조' 카테고리의 다른 글
| [자료구조] 6. 연결 리스트의 응용 (0) | 2022.11.30 |
|---|---|
| [자료구조] 5. 연결리스트 (0) | 2022.11.28 |
| [자료구조] 4. 큐 (1) | 2022.11.25 |
| [자료구조] 3. 스택 (0) | 2022.11.05 |
| [자료구조] 1. 자료구조의 개념 (0) | 2022.11.04 |